Сінгапур уже не перший рік у топі країн за рівнем математичної грамотності 15-річних учнів, що вимірює міжнародне дослідження PISA.
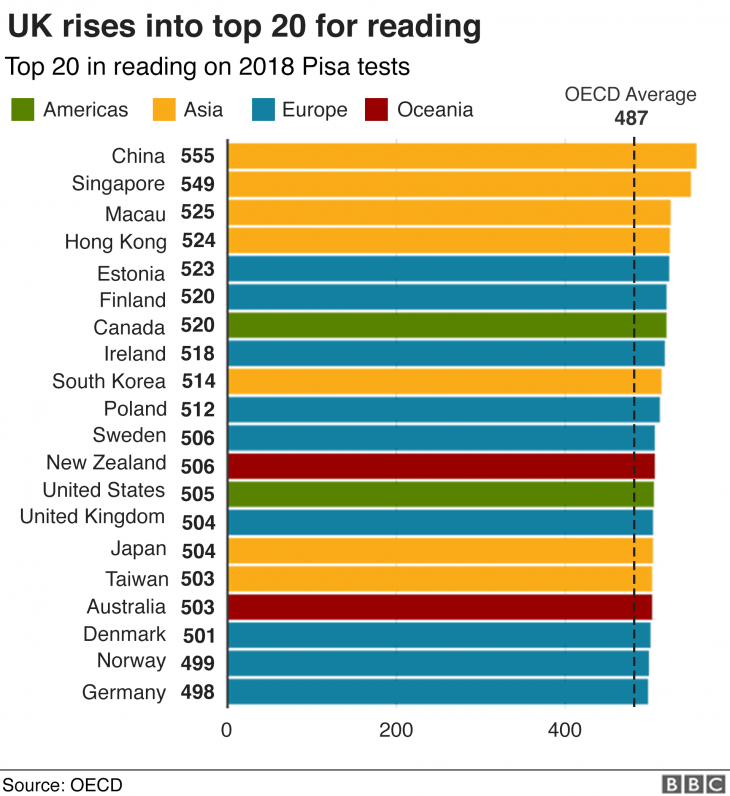
Ілюстрація взята з BBC
Ви натрапите навіть на словосполучення “Сінгапурська математика”, під яким розуміють методику навчання математики, що розробив Національний Інститут освіти Сінгапуру в 1982 році. Методисти Сінгапуру вивчили досвід багатьох країн, проаналізували наявні на той час методики навчання математики і створили свій мікс.
Але на цьому не зупинились. Розробили систему вправ і посібники для учнів та вчителів (у методичних посібниках для вчителів детально описаний кожен крок учителя). Крім того, запровадили постійні моніторинги процесу навчання та навчальних досягнень учнів, що, звісно, слугує передумовами для вдосконалення створеної методики.
ОСНОВНІ ПОЛОЖЕННЯ “СІНГАПУРСЬКОЇ МАТЕМАТИКИ”
- Увага акцентується не на вивченні великих обсягів інформації, а на розумінні учнями базових математичних понять.
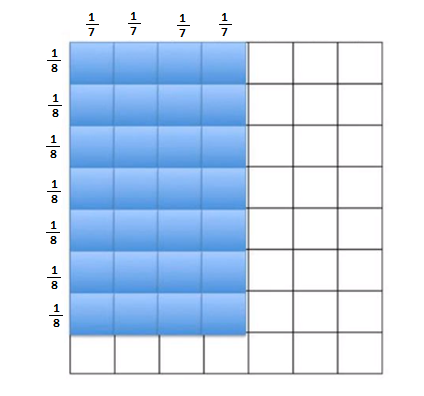
Велика частка часу на уроці виділяється на формування уявлення про поняття. Наприклад, під час вивчення множення дробів говорять не про правило множення, а розглядають і аналізують з учнями його геометричну інтерпретацію.
4/7 * 7/8
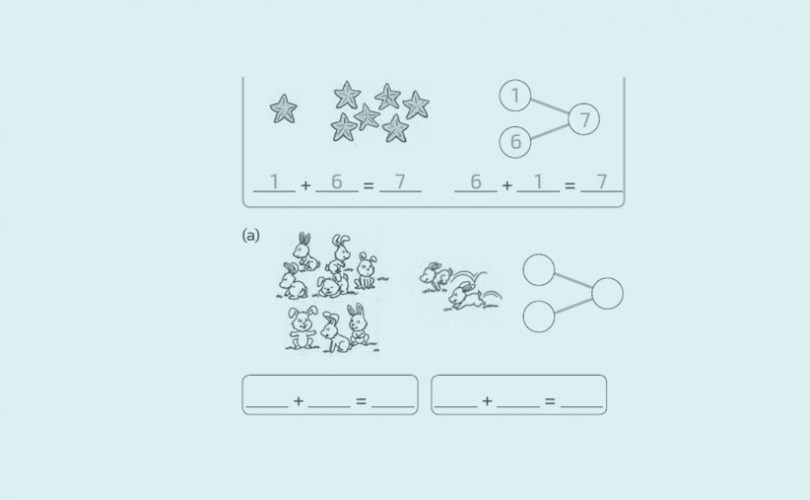
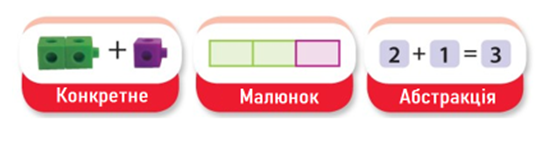
- Будь-яке поняття вводиться від конкретного до абстрактного в три етапи (робота з предметами – робота з малюнками – робота з абстракціями). Наприклад, спершу учні оперують кубиками (3 кубики з’єднують із 6 кубиками й отримують “поїзд” із 9 кубиків), поті аналізують малюнки (3 коти і 6 мишей – це 9 тварин). Після цього переходять до формулювання твердження “3 і 6 буде 9”. І лише після вивчення символів “плюс” та “знаку рівності” переходять до запису рівності 3+6 = 9.
- Навчання будується на розв’язанні життєвих проблемних ситуацій. На початку кожного уроку створюється проблемна ситуація, розв’язання якої учні з учителем мають знайти за допомогою математики. Наприклад, для того, щоби дізнатися улюблений колір своїх подруг, необхідно їх опитати, систематизувати дані і представити їх у зручному вигляді (наприклад, у вигляді діаграми).

- Значна увага приділена моделюванню: і під час викладу вчителем теорії, і під час розв’язування учнями завдань. Учні постійно моделюють проблемні ситуації за допомогою предметів, малюнків чи схем. Під час розв’язування задач надзвичайна увага приділяється створенню до них схем. До створення схем учнів привчають з 1 класу на дуже простих задачах.
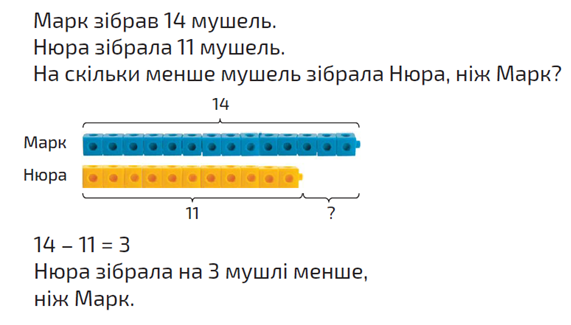
- Неодноразове повторення пройденого матеріалу та на кожному новому рівні – поглиблення знань. Наприклад, спершу учні вивчають зв’язки між числами першого 10, потім на їхній основі складають історії про додавання в межах 10, а потім на основі історій учні вчаться складати й розв’язувати задачі на додавання. Дуже повільне введення понять та неодноразове повторення забезпечує опанування матеріалу кожним учнем відповідно до своїх здібностей і можливостей. Звісно, кожен у своєму темпі. Той, хто швидше опанував матеріал, далі просто тренується. Для цього є спеціальні завдання. А інші мають багато можливостей для усвідомлення та формування правильного уявлення про поняття.
- Використання парних і групових форм навчання. На кожному уроці використовуються різні форми роботи, але переважають парні і групові. Учні в парах обговорюють новий матеріал, виконують практичні роботи, грають в ігри, розв’язують задачі. Наприклад, один учень витягає з коробки дві геометричні фігури, а другий має сказати, чим ці фігури схожі.
- Вітається не запам’ятовування алгоритмів, а пошук власних способів розв’язання завдань.
- Наскрізна лінія вивчення математики в Сінгапурі – розвиток логічного мислення учнів. Наприклад, завдання в посібниках і зошитах, формулюються з мінімальною кількістю слів, але завжди подається приклад виконання завдання, у якому, фактично, прихований код, який треба учню розгадати, і за аналогією виконати решту завдань.
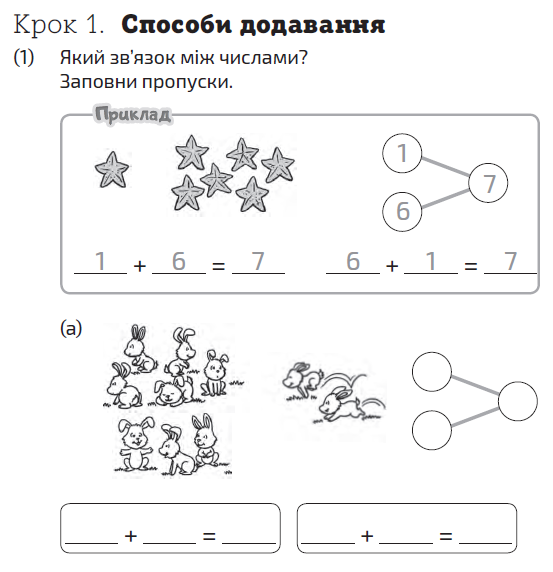
Крім того, у посібниках є окремі рубрики, що спрямовані на розвиток логічного мислення учнів. На розв’язування таких задач можуть виділятися окремі уроки.
- Формування креативного мислення. Часто пропонуються завдання, що не мають однозначної відповіді. Тобто, учні мають перебрати всі варіанти й записати їх. Або вибрати оптимальний. Також учням часто пропонують записати свої вирази чи рівняння, скласти свою історію про додавання чи задачу за певними умовами.
Сінгапурську методику навчання математики вже перейняли, адаптували та впровадили в Японії та Ізраїлі, а також в окремих школах США та Європи. В основі методики математики Сінгапуру лежить особистісно-орієнтований тa діяльнісний підходи. Учні постійно оперують різними предметами (фішками, кубиками, картками, схемами, стрічками, рулетками, у тому числі й цеглинками LEGO) та досліджують зовнішній світ. Організована в такий спосіб легоматематика сприяє розвитку дрібної моторики й на цій основі – мислення.
Це, звісно, впливає і на зацікавленість учнів до вивчення математики. А як ми знаємо, зацікавленість предметом завжди породжує кращі результати учнів у його опануванні.
Дарина Васильєва, ст.н. співробітник відділу математичної та інформатичної освіти Інституту педагогіки НАПН України